2025MBA报考测评申请中......
说明：您只需填写姓名和电话即可免费预约！也可以通过拨打热线免费预约
我们的工作人员会在最短时间内给予您活动安排回复。
导读：形式逻辑那些事
假言命题背后的故事
困惑萌芽
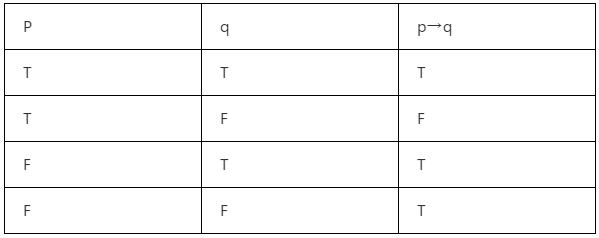
在形式逻辑中，我们学习到复合命题时，有一种命题叫做假言命题，其形式为p→q，真值表形式如下：
通过观察这个表可以发现，只有p真且q假的时候，整个命题的值才为假。
这里应该好理解，我给大家举个简单的小例子：小头爸爸有一天跟大头儿子：如果你期末考试考第一，我就给你买个iPhone 11 Pro Max。当什么情况发生的时候，大头儿子会向围裙妈妈哭诉小头爸爸的承诺不过是一纸空谈。同学们应该都可以想到，这个情况就是：大头儿子考了第一，但是却没给他买iPhone 11 Pro Max
这么说来，p→q这个式子要为假的条件还挺苛刻。但是同学们有没有想过一个问题，p真且q真的情况很直观，但是为什么p为假时，无论q怎样，整个命题都是正确的呢？
这就是我们今天要和大家探讨的问题。
工具准备
同学们上知网搜一下这个问题，这个问题在逻辑学领域中叫做“实质蕴涵悖论”，专家学者们解释的画风基本上如天书一般，有兴趣的同学可以去仔细探索一下，
（推荐一篇张建军教授的文章）
我在这里只提一种管理类联考的形式逻辑的知识体系下的解释模式，希望能帮同学们铲除这一疑难。
要解决这个问题我们要先储备一个工具作为基础知识，该工具的名字叫做：德摩根律
具体用法如下：非(p 且 q)=(非 p)或(非 q)，即￢（p∧q）=￢p∨￢q
非(p 或 q)=(非 p)且(非 q)，即￢（p∨q）=￢p∧￢q
记忆的口诀可以这样描述：每个对象分别否定，连接词“且”与“或”直接转换。
问题解释
现在让我们回到真值表中，找到第二行，也就是p→q为假的唯一的一行，此时p真且q假。
换言之，也就说明，p∧￢q为真，当且仅当，p→q为假，因此p→q与p∧￢q是矛盾的（即真值相反）（回想大头儿子和小头爸爸的故事）。
下一步使用我们的德摩根律对p∧￢q整个取非，即￢（p∧￢q）=￢p∨q,因此￢p∨q与p∧￢q也是矛盾的，到这里其实已经证明完毕了，依据“敌人的敌人是朋友”的原则，我们可以得知：p→q与￢p∨q是等价的。
这时候我们再回到前面的困惑当中，“为什么p为假时，无论q怎样，整个命题都是正确的呢”这个问题便迎刃而解了，根据相容选言命题的性质，一个选言支为真，则整个命题为真，故当￢p为真，￢p∨q为真，p→q自然为真，得证。
总结讨论
这个问题的探讨是很有意义的，不止在逻辑学领域中作为一个非常重要的课题（实质蕴涵悖论）存在，而且在管理类联考逻辑中成为了贯穿复合命题（即假言命题、联言命题和选言命题）的桥梁性公式，相信当你弄懂上述的过程时，你对于管理类联考形式逻辑的认识也会有更系统化的感受。
好了，学到这里，是不是掌握了这个知识点呢？一定要多加练习哦！我们下期见！
