2025MBA报考测评申请中......
说明:您只需填写姓名和电话即可免费预约!也可以通过拨打热线免费预约
我们的工作人员会在最短时间内给予您活动安排回复。
导读:上次给大家集合和函数的基础知识点,这个给大家整理数列的基础知识。
数列
数列是一种特殊的函数,其定义域为全体或部分自然数。
数列的通项公式 A(N)就是一个函数,求出通项公式,等于求出了数列的任一项。
数列的 前 N 项和 S(N)(N=1,2,。。。)构成了一个新的数列,知道 S(N)的公式, 通过 A(1)=S(1),A(N)=S(N)-S(N-1)就能求出原数列的通项公式。
MBA 数学主要考察等差数列和等比数列。有些数列不是等差数列或等比数列,但经过改造后可构造出等差数列或等比数列。
如 A(1)=1, A(N+1)=2A(N)+1。这个数列的每一项都加上 1,就成为等比数列了,通 项公式为 2^N,因此原数列通项公式为:A(N)=2^N-1 其他常见的数列包括 A(N)=N^3, A(N)=N!/(N-K)!, A(N)=1/[N(N-1)]等,都有相应的办法能处理。
数列相关公式
a与S的关系
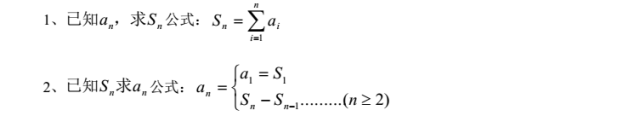

等比数列














